지난주에도 시간이 빠르다고 느꼈지만 벌써 혼공머신도 반!!
Ch.04 다양한 분류 알고리즘
럭키백의 확률을 계산하라!
럭키백에 넣을 생선은 총 7개로,
럭키백에 들어간 생선의 크기, 무게 등이 주어졌을 때 7개 생선에 대한 확률을 출력해야 한다.
(길이, 높이, 두께 외에도 대각선 길이와, 무게 사용 가능!)
K-최근접 이웃(K-NN) 알고리즘을 사용하면?
시간 단축을 위해 결론부터 말하자면 X
과정은 아래를 참고!!
K-최근접 이웃은 주변의 이웃을 참고 하기 떄문에 이웃의 클래스 비율을 확률이라고 출력하면 되지 않을까?
먼저 생선에 대한 정보를 가져오자
import pandas as pd
fish = pd.read_csv('https://bit.ly/fish_csv_data')
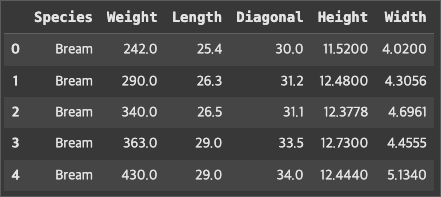
fish.head()< 생선에 대한 데이터 >
그럼 생선의 종류가 뭐뭐 있는지 Species에서 중복 된 생선은 제거 해서 확인해보자.
print(pd.unique(fish['Species']))['Bream' 'Roach' 'Whitefish' 'Parkki' 'Perch' 'Pike' 'Smelt']
중복 된 생선을 제거 후 확인해보았더니 생선은 총 7종이 맞다!
그럼 생선의 데이터를 입력해보자.
Species는 생선의 종류였으니 Species를 제외한 나머지 5개 열을 선택하면 된다.
fish_input = fish[['Weight','Length','Diagonal','Height','Width']]
fish_input.head()
<생선의 입력 데이터>
입력 된 데이터를 확인해보니 생선의 종류를 제외한 데이터가 잘 들어간 것을 확인 할 수있다.
그럼 타겟 데이터를 만들고,
훈련 세트와 테스트 세트로 나눈 뒤 표준화 전처리를 해보자.
fish_target = fish['Species']
# 데이터를 훈련 세트와, 테스트 세트로 나누기
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(fish_input, fish_target, random_state=42)
# 훈련 세트와 테스트 세트를 표준화 전처리
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
자! 그럼 필요한 데이터들이 모두 준비되었다.
이제 할 일은 모델을 훈련시키고, 확률을 예측해보자!!
from sklearn.neighbors import KNeighborsClassifier
# 이웃을 3개로 지정
kn = KNeighborsClassifier(n_neighbors=3)
# 모델 훈련
kn.fit(train_scaled, train_target)
테스트 세트에 있는 처음 5개 샘플의 타깃 값을 예측해보자.
print(kn.predict(test_scaled[:5]))['Perch' 'Smelt' 'Pike' 'Perch' 'Perch']
이 5개 샘플에 대한 예측은 어떤 확률로 만들어 졌는지 확인하기 위해, 샘플에 대한 확률을 출력해보자.
import numpy as np
proba = kn.predict_proba(test_scaled[:5])
print(np.round(proba, decimals=4))[[0. 0. 1. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 1. 0. ]
[0. 0. 0. 1. 0. 0. 0. ]
[0. 0. 0.6667 0. 0.3333 0. 0. ] <- 요놈으로 설명함!!
[0. 0. 0.6667 0. 0.3333 0. 0. ]]
위 결과 값 중 4번째 녀석인 아래의 녀석으로 확인해보자.
[0. 0. 0.6667 0. 0.3333 0. 0. ]
총 7개의 값으로 이루어진 것을 볼 수 있다.
생선의 종류가 7개 였던 것이 기억난다면 이 값들이 어떤 값인지는 추측이 될 것이다!
그럼 맨 앞에서 부터 어떤 생선인지 확인해보자.
print(kn.classes_)['Bream' 'Parkki' 'Perch' 'Pike' 'Roach' 'Smelt' 'Whitefish']
위 값에서는 3번째 생선에 제일 비슷하다고 말하고 있으니 해당 모델은 Perch로 예측을 한 셈이 된다.
그런데 여기서 또!
가만히 생각을 해보니 3개의 이웃을 사용했기 때문에 확률이 0/3, 1/3, 2/3, 3/3이 확률의 전부이다.
확률이라고 하기에는 너무 애매하니 좀 더 좋은 방법을 찾아보자!
로지스틱 회귀
로지스틱 회귀는 간단히 말하자면 어떤 일이 일어날지 말지를 확률로 예측하는 모델이다.
예를 들어 어떤 사람이 물건을 살지 말지, 환자가 병에 걸렸는지 아닌지와 같이 말이다.
선형 회귀와 매우 비슷하지만 선형 회귀는 값을 그대로 예측한다면, 로지스틱 회귀는 0~1 사이의 확률을 예측하여 판단한다.
그렇기 때문에 보통 분류 문제에 쓰는 회귀이다.
그럼 코드로 로지스틱 회귀를 이해해보자!
아래의 코드는 넘파이 배열에서 True, False를 전달하여 행을 선택하는 불리언 인덱싱을 사용한 예제이다.
char_arr = np.array(['A', 'B', 'C', 'D', 'E'])
print(char_arr[[True, False, True, False, False]])['A' 'C']
위 기능을 이용하여 Bream, Smelt을 골라내보자.
# Bream, Smelt 일때만 True를 반환
bream_smelt_indexes = (train_target == 'Bream') | (train_target == 'Smelt')
train_bream_smelt = train_scaled[bream_smelt_indexes]
target_bream_smelt = train_target[bream_smelt_indexes]
# 로지스틱 회귀 모델 훈련
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(train_bream_smelt, target_bream_smelt)
print(lr.predict(train_bream_smelt[:5]))['Bream' 'Smelt' 'Bream' 'Bream' 'Bream']
# 처음 5개 샘플의 예측 확률
print(lr.predict_proba(train_bream_smelt[:5]))[[0.99760007 0.00239993]
[0.02737325 0.97262675]
[0.99486386 0.00513614]
[0.98585047 0.01414953]
[0.99767419 0.00232581]]
로지스틱 회귀로 다중 분류 수행하기
7개의 생선 데이터가 모두 들어있는 train_scaled와 train_target을 사용해보자.
lr = LogisticRegression(C=20, max_iter=1000)
lr.fit(train_scaled, train_target)
print(lr.score(train_scaled, train_target))
print(lr.score(test_scaled, test_target))0.9327731092436975
0.925
결과 값을 보니 훈련 세트와 테스트 세트 모두 점수가 높고, 과대 적합이나 과소 적합도 없는 것으로 보인다.
그럼 이제 샘플들을 예측해보자.
print(lr.predict(test_scaled[:5]))
proba = lr.predict_proba(test_scaled[:5])
print(np.round(proba, decimals=3))['Perch' 'Smelt' 'Pike' 'Roach' 'Perch']
[[0. 0.014 0.842 0. 0.135 0.007 0.003]
[0. 0.003 0.044 0. 0.007 0.946 0. ]
[0. 0. 0.034 0.934 0.015 0.016 0. ]
[0.011 0.034 0.305 0.006 0.567 0. 0.076]
[0. 0. 0.904 0.002 0.089 0.002 0.001]]
확률적 경사 하강법
머신러닝 모델이 학습할 때, 오차를 줄이기 위해 조금씩 가중치를 조정하는 방법
확률적 경사 하강법은, 가중치를 천천히 바꾸면서 정답에 가까워지도록 만드는 방법이다.
그런데 왜?! "확률적"이라는 말이 들어갈까?
그것은 바로. 전체 데이터를 가지고 계산하면 느리기 때문에!! 랜덤하게 딱 하나의 데이터를 골라서 가중치를 업데이트 하기 때문이다.
확률적 경사 하강법에서 훈련 세트를 한 번 모두 사용하는 것은 에포크라고 부르며,
여러개의 샘플을 사용해 경사 하강법을 수행하는 방식은 미니배치 경사 하강법, 전체 샘플을 사용하는 것은 배치 경사 하강법이라고 부른다.
손실 함수
모델이 예측한 값이 정답과 얼마나 다른지를 숫자로 알려주는 함수!
손실 함수를 직접 만들거나, 계산하는 일은 거의 없다. 왜냐! 바로 머신러닝 라이브러리가 처리해주니까!
하지만 정의를 왜 해야하는지는 중요하기 때문에 확률적 경사 하강법을 사용해 만들어보자.
SGDClassifier
import pandas as pd
fish = pd.read_csv('https://bit.ly/fish_csv_data')
fish_input = fish[['Weight','Length','Diagonal','Height','Width']]
fish_target = fish['Species']
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(fish_input, fish_target, random_state=42)
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
# SGDClassifer
from sklearn.linear_model import SGDClassifier
sc = SGDClassifier(loss='log_loss', max_iter=10, random_state=42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
# 1 에포크 씩 이어서 훈련
sc.partial_fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))0.773109243697479
0.775
# 1 에포크씩 이어서 훈련
0.7983193277310925
0.775
에포크와 과대/과소 적합
확률적 경사 하강법을 사용한 모델은 에포크 횟수에 따라 과소적합이나 과대적합이 될 수 있다.
왜 그럴까?
에포크 횟수가 적은 경우 마치 산을 다 내려오지 못하고 훈련을 마치는 것과 같이 덜 학습하게 되고,
횟수가 많은 경우는 훈련 세트에 너무 잘 맞아 나쁜 과대적합된 모델일 가능성이 높다!
그럼 그래프로 확인해보자.
import numpy as np
sc = SGDClassifier(loss='log_loss', random_state=42)
train_score = []
test_score = []
classes = np.unique(train_target)
# 에포크 300번 반복
for _ in range(0, 300):
sc.partial_fit(train_scaled, train_target, classes=classes)
train_score.append(sc.score(train_scaled, train_target))
test_score.append(sc.score(test_scaled, test_target))
# 그래프화
import matplotlib.pyplot as plt
plt.plot(train_score)
plt.plot(test_score)
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()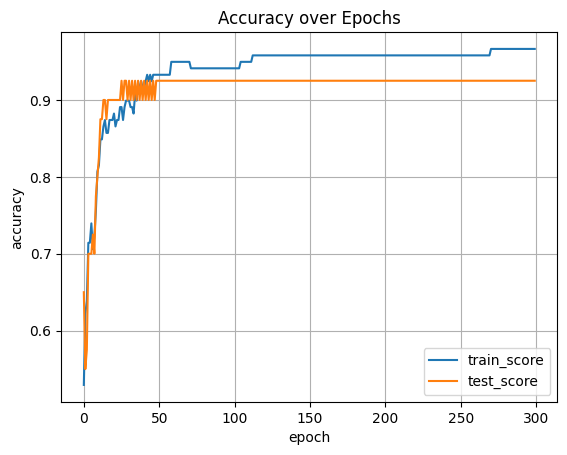
데이터가 작기 때문에 아주 잘 드러나지는 않지만,
에포크 초기에는 과소적합되어 훈련 세트와 테스트 세트의 점수가 낮고,
100번 째 에포크 이후에는 훈련 세트와 테스트 세트의 점수가 조금씩 벌어지고있다.
그렇기 때문에 해당 모델은 약 100번 정도의 에포크가 적절한 반복 횟수로 보인다.
숙제
기본 숙제
4-1 확인문제 2. 로지스틱 회귀가 이진 분류에서 확률을 출력하기 위해 사용하는 함수는 무엇인가요?
[ v ] . 시그모이드 함수
[ ]. 소프트맥스 함수
[ ]. 로그 함수
[ ]. 지수 함수
'Newb > 머신러닝' 카테고리의 다른 글
| [혼공머신] 6주차 [6/6] (8) | 2025.08.15 |
|---|---|
| [혼공머신] 5주차 [5/6] (13) | 2025.08.09 |
| [혼공머신] 4주차 [4/6] (3) | 2025.07.27 |
| [혼공머신] 2주차 (11) | 2025.07.13 |
| [혼공머신] 1주차 (2) | 2025.07.06 |